May 15th

TRIGONOMETRY
 We´ve studied the basics and we are now solving right-angled triangles (right triangles in American English). Here it´s one resolved example:
 
And a couple of exercises, from our old friend, the BBC Bitesize (by the way, on those exercises, "sf" stands for significant figures).

Now you have a chance to practice:
1. An activity.
2. A first test.

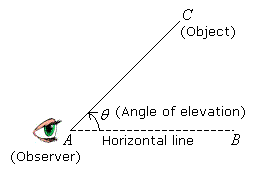
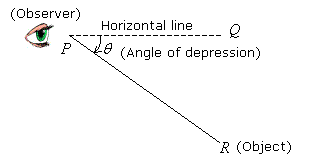
Angles of elevation and depression
Those two concepts are going to appear very often in Trigonometry problems. Here it's an explanation:

And now a couple of example problems:




Have a look now at this video about how useful is Trigonometry for airplane pilots:
Proposed problems

Trig Word Problems

View another webinar from Kristen T

EXTRA!
Remember the trig ratio definitions singing:

April 24th

TRIANGLE SIMILARITY CRITERIA
First a quick reminder of the similarity criteria for triangles, with these examples:


And now it´s time for some practice:
1. A first test.
2. In this test we will use the Basic Proportionality Theorem, also called the Thales Theorem.
3. A third test.
4. Last 18-question test.

April 10th

We are studying now COMBINATORICS. We´ve already learned all the basic concepts and formulas, but you can watch this video to remember a couple of things:


And now it´s time for some exercises and tests:

1. About permutations, try problems 1 to 6 on this page (and yes!, I know there are 2 different number 5s).

2. About combinations, try problems 1 to 5 here.

3. A first test, very easy (skip the last question).

March 13th

PROBABILITY
We have studied all of the probability´s basic concepts. Now it´s time to put that knowledge to the test with the following activities:
- An interactive activity (with the headphones).
- A 10-question test (includes questions about independent events).
- A "Bitesize" test (an easy one).
- A game from a Canadian site Toads and Vines. The vines will take you up, the toads tongues will take you down, so try to avoid them. Answering the questions correctly will get you turns in the spinner or the dice. Try it, it´s not difficult.
- A second "Bitesize" test (and yes, it´s a little more difficult).
- And a last one. Be careful: the first questions are simple, but the last ones require you to use conditional probability.

February 7th

Let´s continue with statistics:

First of all, check this test about graphs now (if you couldn´t do it last week).

MEASURES OF CENTRAL TENDENCY
We´ve already learned what Sigma Notation was. You can practice it with these exercises.

Remember the definitions with this activity or check this video again:



Now you can practice the central tendency measures at the Museum of Aztec Art.
And finally a test.

January 31st

Today it´s about statistics.

Collecting data
Listen to this and solve the activity about tables and bar charts.
A first test.

GRAPHS AND DIAGRAMS
About pie charts: learn here what a pie chart is and how you draw one .

1. With Valentine´s Day just around the corner, this exercise just seemed appropiate: try and answer the questions.
2. And one with some vocabulary.

We can draw graphs using OpenOffice´s Calc:
After selecting the data on the spreadsheet, go to "Insert" and then "Chart". Select the kind of graph you´re interested in and the program would do the rest. You can modify the graph by addind a title, changing colors or the legend, etcetera.
3. Use the data on the page to draw a first pie chart
4. Use the data on the page to draw a second pie chart


About bar charts:
5. Complete the sentences on this one.
6. Use the data on exercise 3 to draw a bar chart using Calc.


About frequency polygons:
- An activity about frequency polygons (and more).
- And learn how to draw one (with grouped data):


And finally, a very, very easy test about graphs.

January 10th

Inequalities
As you already know, we use the following symbols:


Solving inequalities
"Solving'' an inequality means finding all of its solutions. A "solution'' of an inequality is a number which when substituted for the variable makes the inequality a true statement.
For example: 2 is a solution of 2x-3<5 because 2·2-3<5

When solving inequalities, there are certain manipulations of the inequality which do not change the solutions:

Rule 1. Adding/subtracting the same number on both sides.

Rule 2. Multiplying/dividing by the same POSITIVE number on both sides.

Rule 3. Multiplying/dividing by the same NEGATIVE number on both sides AND changing the orientation of the inequality sign.

ALWAYS EXPRESS SOLUTIONS AS AN INTERVAL(S)